Happy 164th birthday, Aleksandr Lyapunov!

I recently participated in the first annual Manim math animation engine hackathon! The theme was anniversaries, so I created the above animation to celebrate the 164th anniversary of mathematician Aleksandr Lyapunov’s birth. This extended some ideas I presented from Steven Strogatz’s nonlinear dynamics textbook at the University of Minnesota’s math directed reading program symposium. Here’s the source code for the animation and visualizations.

The math

Consider the system

$$ \begin{aligned} \frac{dx}{dt} &= y-x^3 \newline \frac{dy}{dt} &= -x-y^3. \end{aligned} $$

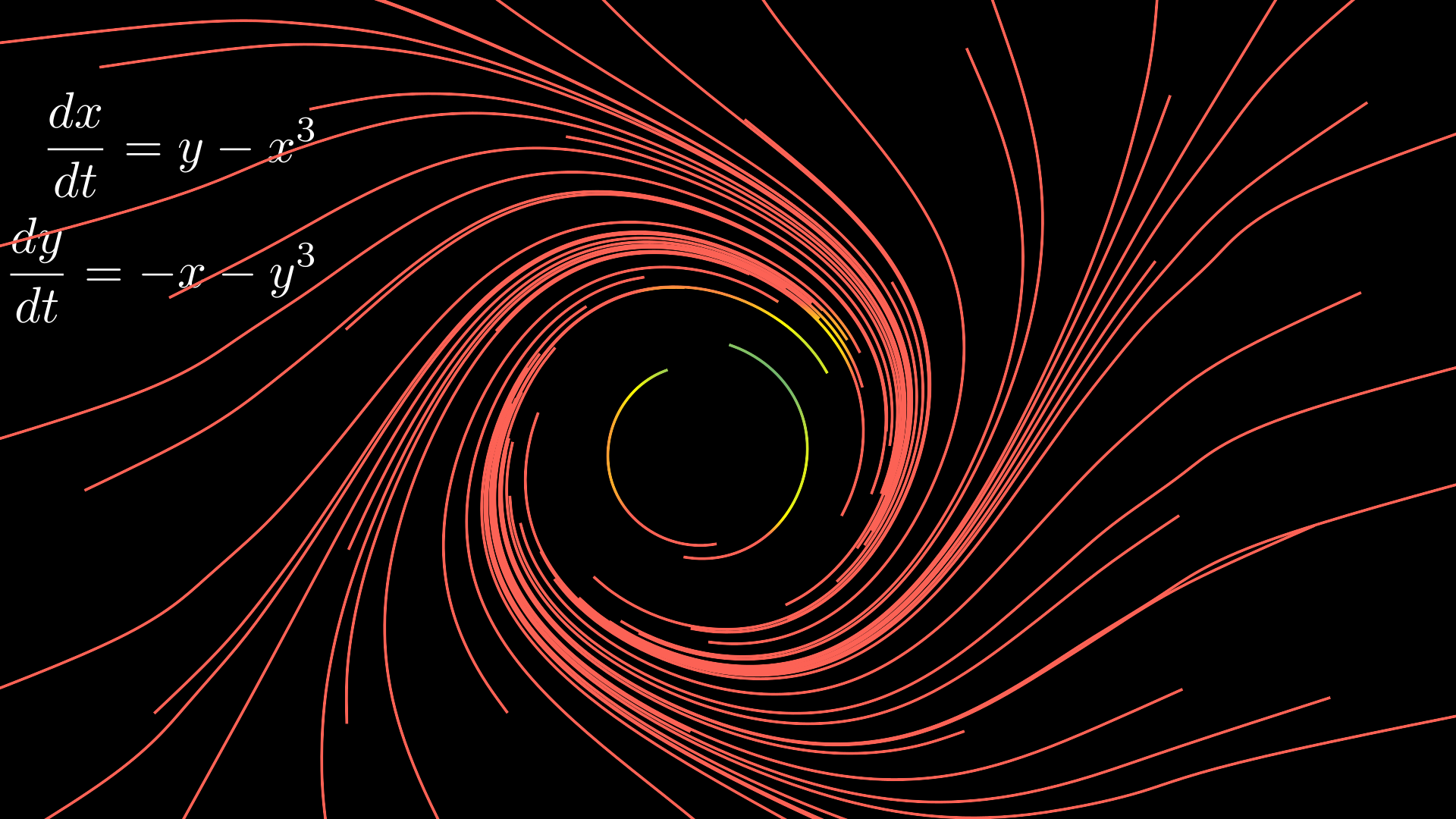Our dynamical system

We can’t use linearization about the fixed point at the origin to determine its stability; the Jacobian has pure imaginary eigenvalues, so the linearization is not robust to small nonlinear terms.

However, Lyapunov showed that finding a Lyapunov function \(V\) which is locally positive definite and has a locally negative definite time derivative implies stability. This is similar to an energy function as the trajectories move monotonically down the basin of \(V\). Let’s try \(V = x^2 + y^2\) for the system.

The chosen Lyapunov function

$$ \begin{aligned} \frac{dV}{dt} &= \frac{dV}{dx} \frac{dx}{dt} + \frac{dV}{dy} \frac{dy}{dt} \newline &= 2x(y-x^3) + 2y(-x-y^3) \newline &= 2xy -2x^4 - 2yx -2y^4 \newline &= -2x^4 - 2y^4 \end{aligned} $$

\(V\) is non negative and \(\frac{dV}{dt}\) is non positive, so it truly is a Lyapunov function. Its existence implies that the system is asymptotically stable; trajectories all eventually converge to the origin.

So the key insight that Lyapunov found was that there doesn’t need to be a real energy function, nor does a system have to be physical; all you need is a Lyapunov function that satisfies a few properties to determine its stability.

Outside of this toy example, Lyapunov functions are used in the engineering of nonlinear control systems. Their analogue in control-Lyapunov functions has been used in robotics for path planning around obstacles.